for loop <<
Previous Mass-Spring-Damping
原始碼:
// 下列 Dart 程式, 利用 Runge Kutta 迭代運算法, 解常微分方程式
// 設 t 為時間, x 則設為物體的位移
// 假設要解 F=ma 的單一質量加上彈簧 (常數為 k) 與黏滯阻尼 (常數為 b)
// f 為沿位移方向的施力
// dx/dt = v, dv/dt = (f-kx-bv)/m
// dx / dt = (t - x)/2, 起始值 t0=0, x0=1, 求 t=2 時的 x 值
//
// 已知起始值 t0 與 x0 後, 可以利用下列 rungeKutta 函式, 以
// h 為每步階增量值, 求 dxdt 常微分方程式任一 t 的對應值 x
// 定義函式 rungeKutta, 共有四個輸入變數
// 物體質量
const num m = 1;
// 對質量的施力 f
const num f = 0.0;
// 彈簧係數
const num k = 1;
// 阻尼係數
const num b = 1;
// 呼叫運算時, 需要起始時間, 終點時間, 位移起始值與速度起始值, 增量 h
rungeKutta(t0, x0, v0, t, h) {
// 利用步階增量值 h 與 t 的起始及終點值
// 計算需要迭代的次數 n
int n = ((t - t0) / h).toInt();
// 宣告 x 為雙浮點數, 且設為起始值 x0
double x = x0;
// 宣告 v 為雙浮點數, 且設為起始值 v0
double v = v0;
// 模擬運算前, 列出起始條件
// 只列到小數點第三位, 時間、位移與速度以 \t 隔開, \t 代表插入 tab 符號, 可將資料複製到 Excel 進行繪圖
print("${t0.toStringAsFixed(3)} \t ${x.toStringAsFixed(3)} \t ${v.toStringAsFixed(3)}");
// 利用已知的 t0, x0, t 終點值與步階增量值 h, 迭代求 x 對應值
// 索引值 i 將每次增量 1, 從 i=1 執行 for 環圈至 i=n
for (int i = 1; i <= n; i++) {
// 將此階段的 t 與 x 值代入 dxdt 與 dvdt 函式求下列四個浮點變數值
// 因為必須兩個函式耦合, 必須同時計算
double xk1 = h * dxdt(t0, x, v);
double vk1 = h * dvdt(t0, x, v);
double xk2 = h * dxdt(t0 + 0.5 * h, x + 0.5 * xk1, v + 0.5 * vk1);
double vk2 = h * dvdt(t0 + 0.5 * h, x + 0.5 * xk1, v + 0.5 * vk1);
double xk3 = h * dxdt(t0 + 0.5 * h, x + 0.5 * xk2, v + 0.5 * vk2);
double vk3 = h * dvdt(t0 + 0.5 * h, x + 0.5 * xk2, v + 0.5 * vk2);
double xk4 = h * dxdt(t0 + h, x + xk3, v + vk3);
double vk4 = h * dvdt(t0 + h, x + xk3, v + vk3);
// 利用上述四個變數值求此步階增量後的對應 x 值
x = x + (1.0 / 6.0) * (xk1 + 2 * xk2 + 2 * xk3 + xk4);
v = v + (1.0 / 6.0) * (vk1 + 2 * vk2 + 2 * vk3 + vk4);
// 每次 for 迴圈執行最後, 準備計算下一個步階增量後的 x 對應值
// t 起始值配合步階增量值 h, 進行增量
t0 = t0 + h;
// 列出各模擬運算時間點所得到的結果
// 只列到小數點第三位, 時間、位移與速度以 \t 隔開, \t 代表插入 tab 符號, 可將資料複製到 Excel 進行繪圖
print("${t0.toStringAsFixed(3)} \t ${x.toStringAsFixed(3)} \t ${v.toStringAsFixed(3)}");
}
// 完成 for 迴圈迭代後, 傳回與 t 終點值對應的 x 值
return [x, v];
}
// 將微分方程式 "dx / dt = v" 定義為 dxdt 函式
dxdt(t, x, v) {
return v;
}
// dx/dt = v, dv/dt = (f-kx-bv)/m
dvdt(t, x, v) {
return (f - k * x - b * v) / m;
}
// 定義 main() 主函式內容, 目的在利用 rungeKutta 函式
// 解常微分方程式
main() {
// Driver method
// num 資料型別可以是整數或雙浮點數
num t0 = 0;
num x0 = 1;
num v0 = 0;
num t = 5;
double h = 0.1;
rungeKutta(t0, x0, v0, t, h);
}
dartpad:
曲線圖:
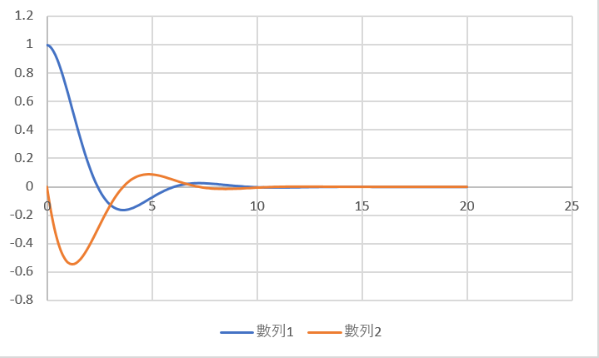
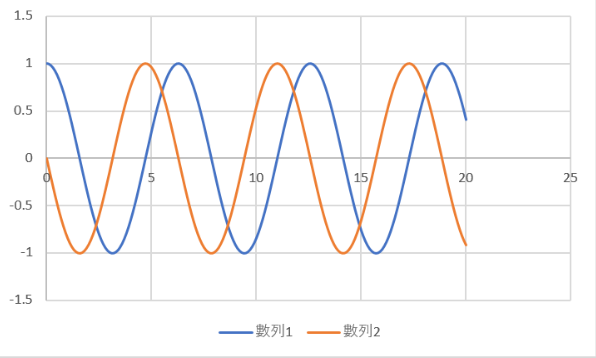
for loop <<
Previous